Which Construction Can You Use To Prove The Pythagorean Theorem Based On Similarity Of Triangles?
Pythagorean Theorem Calculator
Pythagorean Theorem for Right Triangles
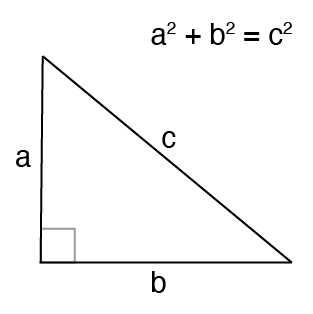
a = side leg a
b = side leg b
c = hypotenuse
A = expanse
What is the Pythagorean Theorem?
The Pythagorean Theorem states that the sum of the squared sides of a right triangle equals the length of the hypotenuse squared.
Yous might recognize this theorem in the form of the Pythagorean equation:
\[ a^{2} + b^{two} = c^{2} \]
If you know the length of any 2 sides of a right triangle you tin can employ the Pythagorean equation formula to discover the length of the third side.
Calculator Utilize
This calculator solves the Pythagorean Theorem equation for sides a or b, or the hypotenuse c. The hypotenuse is the side of the triangle opposite the right angle.
For right triangles only, enter any two values to find the third. See the solution with steps using the Pythagorean Theorem formula.
This calculator also finds the area A of the correct triangle with sides a and b. The formula for expanse of a right triangle is:
\[ A = \dfrac {ab}{2} \]
Pythagorean Theorem Formula
Using the Pythagorean Theorem formula for correct triangles yous can discover the length of the third side if you know the length of any ii other sides. Read below to run across solution formulas derived from the Pythagorean Theorem formula:
\[ a^{2} + b^{2} = c^{2} \]
Solve for the Length of the Hypotenuse c
The length of the hypotenuse is the square root of the sum of the sides squared.
\[ c = \sqrt{a^{2} + b^{two}} \]
Solve for Length of Side a
The length of side a is the square root of the squared hypotenuse minus the square of side b.
\[ a = \sqrt{c^{2} - b^{two}} \]
Solve for the Length of Side b
The length of side b is the foursquare root of the squared hypotenuse minus the square of side a.
\[ b = \sqrt{c^{two} - a^{2}} \]
Solve for Expanse A of the Right Triangle
The area of a right triangle is side a multiplied by side b divided by 2.
\[ A = \dfrac {ab}{2} \]
What are Pythagorean Triples?
A Pythagorean triple is a set of three positive integers for sides a and b and hypotenuse c that satisfy the Pythagorean Theorem formula a2 + b2 = c2
The smallest known Pythagorean triple is 3, four, and five. Showing the work:
\[ a^{2} + b^{2} = c^{2} \] \[ iii^{ii} + four^{2} = 5^{ii} \] \[ 9 + 16 = 25 \] \[ 25 = 25 \]
References:
Weisstein, Eric W. "Pythagorean Theorem" From MathWorld--A Wolfram Web Resource. Pythagorean Theorem.
Wikipedia "Pythagorean Theorem" at https://en.wikipedia.org/wiki/Pythagorean_theorem last accessed May 4, 2020.
Follow CalculatorSoup:
![]()
![]()
Which Construction Can You Use To Prove The Pythagorean Theorem Based On Similarity Of Triangles?,
Source: https://www.calculatorsoup.com/calculators/geometry-plane/pythagorean-theorem.php
Posted by: stanfordsulthen01.blogspot.com


0 Response to "Which Construction Can You Use To Prove The Pythagorean Theorem Based On Similarity Of Triangles?"
Post a Comment